区间$\text{DP}$比线性$\text{DP}$好想一些。
对于一道典型的区间$\text{DP}$问题,我们很容易思考到如何划分区间(集合)?
显然,最小的区间是每个数本身,此时合并花费一定最少(因为不需要花费)
考虑两个数作为一个区间,此时无论怎么合并花费一定最少(只有一种合并方法)
对于三个数及以上显然不存在直接合并一定最少的情况,例如 $1,3,100$ 如果先合并 $3,100$ 再合并 $1,103$ 总花费是 $207$ ,先合并 $1,3$ 再合并 $4,100$ 总花费则为 $108$。
那我们可以一直划分一个长度大于等于三的区间,那么显然前一部分的最小加上后一部分的最小使得总体最小,满足最优子结构
其中 $f(i,j)$ 表示合并 $i\sim j$ 的最小花费 $cost(i,j)$ 为合并 $i,j$ 的最小代价
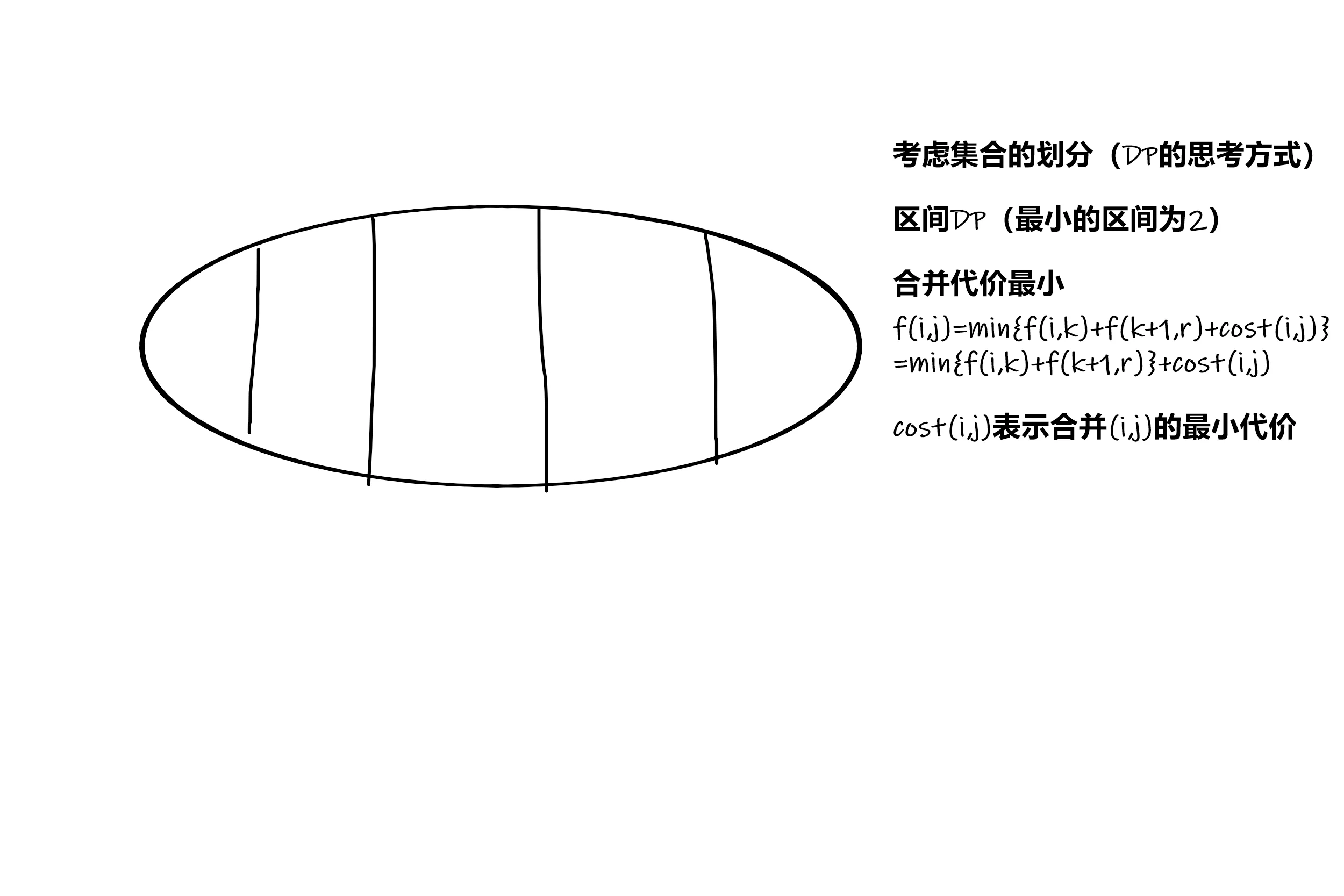
想知道 $cost(i,j)$ 可以采用前缀和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| #include <bits/stdc++.h>
using namespace std;
int n,a[305],b[305],f[305][305];
int main() {
memset(f,0x3f,sizeof(f));
scanf("%d",&n);
for(int i=1;i<=n;i++) {
scanf("%d",&a[i]);
b[i]=b[i-1]+a[i],f[i][i]=0;
}
for(int len=1;len<n;len++)
for(int l=1;l+len<=n;l++) {
int r=len+l;
for(int k=1;k<r;k++)
f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+b[r]-b[l-1]);
}
printf("%d",f[1][n]);
return 0;
}
|
枚举每一个长度 $\text{len}$ 的序列的最小合并花费,最终求出 $f(1,n)$ 即最终的最小花费。
有了上一题的经验,很容易知道这一题的结论也是 $f(i,j) = \min \{ f(i,k) + f(k+1,r) \} + sum(i,j)$
难点在于环形,我们可以用一个简单的办法解决,原序列展开最多 $n$ 的长度,我们只需要把整个序列复制一遍使其能够计算到 $2n$ 的位置就可以了
a[i+n]=a[i];
对于最大值和最小值可以开两个数组 f, g 来解决,本质是一样的,但是要枚举每次长度为 $n$ 的序列的起始点才能找到最大值和最小值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| #include <bits/stdc++.h>
using namespace std;
int n,a[605],b[605],f[605][605],g[605][605],res1=0x7fffff,res2;
int main() {
memset(f,0x3f,sizeof(f));
scanf("%d",&n);
for(int i=1;i<=n;i++) {
scanf("%d",&a[i]);
a[i+n]=a[i];
}
for(int i=1;i<=n*2;i++) b[i]=b[i-1]+a[i],f[i][i]=g[i][i]=0;
for(int len=1;len<n;len++) {
for(int l=1;l+len<=n*2;l++) {
int r=l+len;
for(int k=l;k<r;k++)
f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+b[r]-b[l-1]);
g[l][r]=max(g[l][r],g[l][k]+g[k+1][r]+b[r]-b[l-1]);
}
}
for(int i=1;i<=n;i++) res1=min(res1,f[i][i+n-1]),res2=max(res2,g[i][i+n-1]);
printf("%d\n%d",res1,res2);
return 0;
}
|
为什么树也是区间$\text{DP}$?
这里运用了中序遍历的性质(拍扁序)直接成为了一个区间
每次如果能够更新则根的序号改变。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| #include <bits/stdc++.h>
using namespace std;
int n,a[35],f[35][35],g[35][35];
void dfs(int l,int r) {
if(l>r)
return;
printf("%d ",g[l][r]);
dfs(l,g[l][r]-1);
dfs(g[l][r]+1,r);
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++) {
scanf("%d",&a[i]);
f[i][i]=a[i];
g[i][i]=i;
}
for(int len=1;len<n;len++) {
for(int l=1;l+len<=n;l++) {
int r=l+len;
for(int k=l;k<=r;k++) {
if(k==l) {
if(f[l][r]<a[l]+f[k+1][r])
f[l][r]=a[l]+f[k+1][r],g[l][r]=k;
}
else if(k==r) {
if(f[l][r]<a[r]+f[l][k-1])
f[l][r]=a[r]+f[l][k-1],g[l][r]=k;
}
else {
if(f[l][r]<a[k]+f[l][k-1]*f[k+1][r])
f[l][r]=a[k]+f[l][k-1]*f[k+1][r],g[l][r]=k;
}
}
}
}
printf("%d\n",f[1][n]);
dfs(1,n);
return 0;
}
|
限于作者本人能力有限,期待各位多提些建议

