初赛过了

CSP/S-2019

​ Dijkstra 需要选取最近的 d[s]，Floyd 不需要任何贪心，Prim 同 Dijkstra，Kruskal 需要选取最短的边

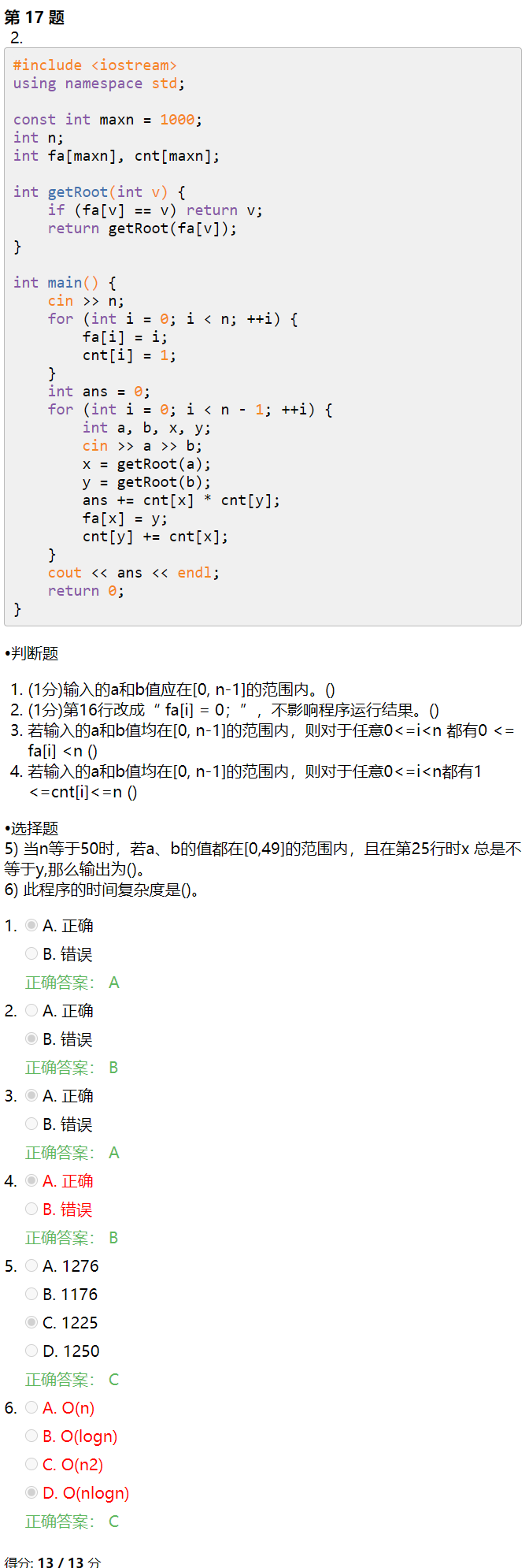
第 4 题中，如果给定 $a=b$，那么 cnt[i] 会变成原先的两倍可能会超出 $n$
第 6 题中，要知道并查集不带路径压缩的最坏时间复杂度是 $\mathcal O(n)$ 的，那么执行 $n$ 次也就是 $\mathcal O(n^2)$ 的

模拟题自测

3、下列说法错误的是（）。
A、栈和队列的存储方式既可是顺序方式，也可是链式方式
B、线性表在物理存储空间中不一定是连续的
C、二叉树中每个节点的两棵子树高度差为1
D、对于一棵非空二叉树，它的根节点作为第一层，则第i层至多有2^(i-1)个节点

​ 显然选 C，因为很容易举出反例。

memset(a,255,sizeof(a)) 等价于将 a 全部赋值为 $-1$

一些知识点总结

局域网、城域网、广域网、个人局域网

• LAN：局域网
• MAN：城域网
• WAN：广域网
• PAN：个人局域网

RAM 中的信息是 计算机工作时随机写入的（NOIP2000 普及）

用静电吸附墨粉后转移到纸张上，是 激光打印机 的工作方式（NOIP 2004）

彩色图像以位图形式保存时，若色深为 $n$，分辨率为 $x \times y$，则为 $n \times x \times y$ bit

• 1B=8bit
• 1KB=1024B
• 1MB=1024KB
• 1GB=1024MB
• 1TB=1024GB

二叉树的若干性质

• 在二叉树的第 $i$ 层上最多有 $2^{i-1}$ 个结点（$i \ge 1$）
• 深度为 $k$ 的二叉树至多有 $2^{k} - 1$ 个结点（满二叉树）
• 对于任意一棵二叉树，如果其叶结点数为 $n_0$，而度数为 $2$ 的结点总数为 $n_2$，则有 $n_0=n_2+1$
• 具有 $n$ 个结点的完全二叉树的深度为 $\lfloor \log_2n \rfloor+1$

遍历二叉树

前序遍历：根结点 左子树 右子树
中序遍历：左子树 根结点 右子树
后序遍历：左子树 右子树 根结点

知前序、中序

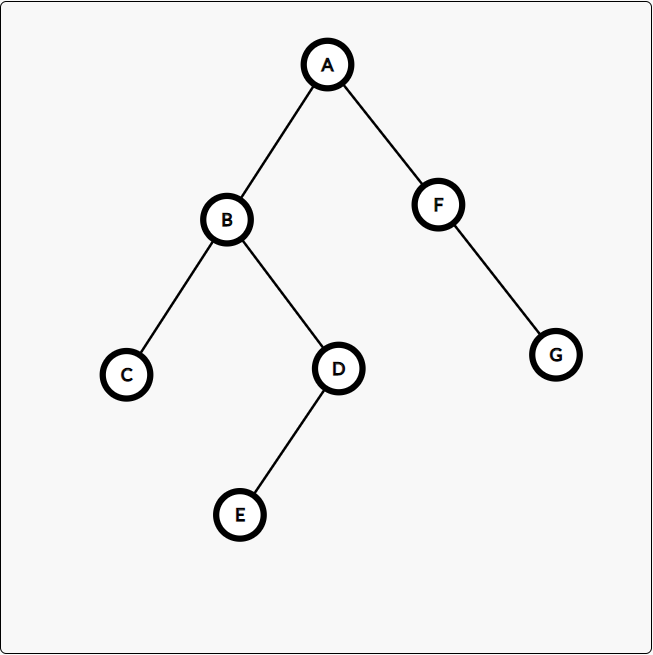
前序：ABCDEFG
中序：CBEDAFG
前序找到 A 为根，在中序中找到左子树 BCDE、右子树 FG
前序找到 B 为根，在中序中找到左子树 C、右子树 DE
前序找到 D 为根，在中序中找到左子树 E、无右子树
前序找到 F 为根，在中序中找到右子树 G、无左子树

知后序、中序

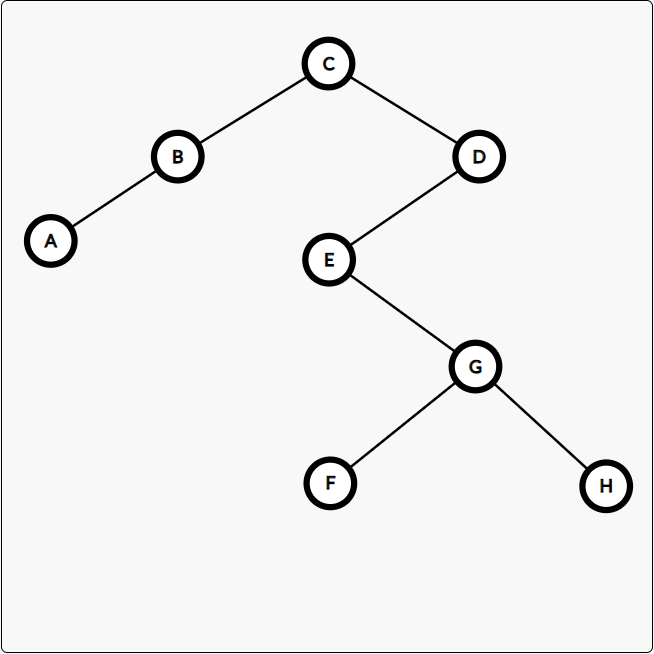
后序：ABFHGEDC
中序：ABCEFGHD
后序找到 C 为根，在中序中找到左子树 AB、右子树 EFGHD
后序找到 B 为根，在中序中找到左子树 A、无右子树
后序找到 D 为根，在中序中找到左子树 EFGH、无右子树
后序找到 E 为根，在中序中找到右子树 FGH、无左子树
后序找到 G 为根，在中序中找到左子树 F、右子树 H

排列组合

$$P_n^k=\dfrac{n!}{(n-k)!}\\ C_{n}^{k}=\binom{n}{k}=\dfrac{P_{n}^{k}}{P_{k}^{k}}=\dfrac{n!}{k!(n-k)!}\\ S(n,m)=\begin {Bmatrix} n \\ m\end {Bmatrix}={\frac 1 {m!}}\sum_{k=0}^m (-1)^k\binom{m}{k}(m-k)^n \\$$ $${\binom{7}{2}}$$