原题链接

官方题解

题目描述

我有一张 $n$ 个节点的无向边带权图。它的边很多，用这个方法表示：

• 有 $k$ 个集合；第 $i$ 个集合可以表示为 $Si={(T_1,W_1),(T_2,W_2),\dots,(T{|Si|},W{|S_i|})}$。
• 对于任何两对 $(T_i,W_i),(T_j,W_j)$ 在同一个集合里面，图中会形成一条连 $T_i$ 和 $T_j$ 的边，边权为 $W_i+W_j$。

请对于所有节点 $i$ 找到 $1$ 到 $i$ 的最短路，即从 $1$ 到 $i$ 的边权和最小的简单路径。

输入格式

第一行两个正整数 $n,k$。
接下来描述 $k$ 个集合。
第 $i$ 集合的描述的第一行一个正整数 $|S_i|$，表示 $|S_i|$ 的大小。
接下来 $S_i$ 行，每行两个正整数 $t,w$，表示 $(t,w)\in S_i$。

对于前 $10\%$ 的数据，$|S_i|=2$；
对于前 $20\%$ 的数据，$|S_i|\le10$；
对于前 $50\%$ 的数据，$|N|\le1000,\sum|S_i|\le2000$；
对于 $100\%$ 的数据，$1\le|N|\le2\cdot10^5,\sum|S_i|\le4\cdot10^5,0\le W_i\le10^9$。

输出格式

一行 $n$ 个正整数；第 $i$ 个正整数表示 $1$ 到 $i$ 的最短路长度。如果不存在一条路径，输出 $\textsf{0x3f3f3f3f3f3f3f3f}=4557430888798830399$。

题解

1. 暴力建图，跑 Dijkstra，可以通过前 $50\%$ 的数据

2. 对于 $100\%$ 的数据，仍然使用暴力建图并采用优先队列优化的 Dijkstra 就是 $\mathcal{O}(\sum |S^2_i| \log \sum |S^2_i|)$ 的复杂度，不能接受，考虑如何优化建图。

   每个集合中所有点总要两两连边，这样边数是 $|S^2| - |S|$($\dfrac{|S| \times (|S|-1)}{2} \times 2$)的，将其转换一下，对于每一个集合设立一个中间点，所有的点 $T_i$ 向其连一条边权为 $W_i$ 的边，和原图实际上是等价的，边数变成了 $2|S|$。

   以样例为例：

   

   

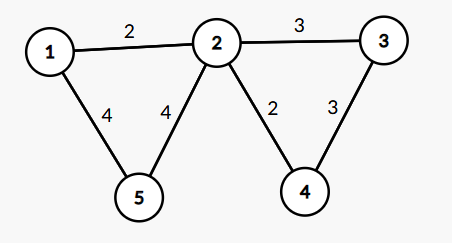
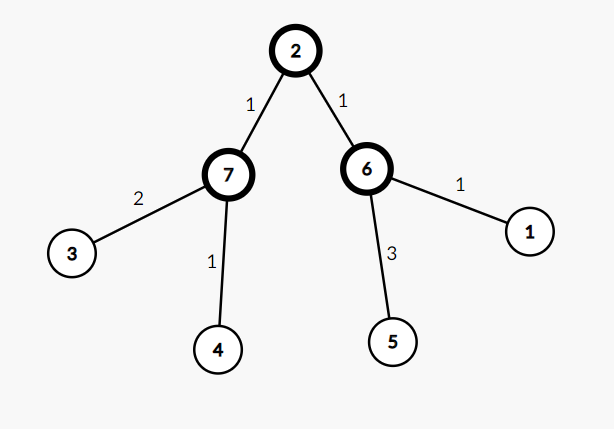
代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 4e5 + 5, M = N << 2;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int tot, head[N], to[M], nxt[M];
bool vis[N];
ll cst[M], dis[N], b[N];
int n, k, siz, x;
ll y;
int Mid;
struct Node {
    ll x, dis;
    bool operator<(const Node &rhs) const { return rhs.dis < dis; }
};
void add(int x, int y, ll z) { to[++tot] = y, cst[tot] = z, nxt[tot] = head[x], head[x] = tot; }
void dij(int u) {
    priority_queue<Node> q;
    for (int i = 1; i <= Mid; i++) dis[i] = INF;
    dis[u] = 0;
    q.push(Node{ u, 0 });
    while (!q.empty()) {
        int t = q.top().x;
        q.pop();
        if (vis[t]) continue;
        vis[t] = 1;
        for (int i = head[t]; i; i = nxt[i]) {
            int v = to[i];
            if (dis[v] > dis[t] + cst[i]) {
                dis[v] = dis[t] + cst[i];
                if (!vis[v]) q.push(Node{ v, dis[v] });
            }
        }
    }
}
int main() {
    cin >> n >> k;
    Mid = n;
    for (int i = 1; i <= k; i++) {
        cin >> siz;
        Mid++;
        for (int j = 1; j <= siz; j++) {
            cin >> x >> b[j];
            add(x, Mid, b[j]);
            add(Mid, x, b[j]);
        }
    }
    dij(1);
    for (int i = 1; i <= n; i++) cout << dis[i] << " ";
    return 0;
}

注意

1. 本题需要 long long
2. 图不一定联通
3. 每一个集合的中间点都是不同的（代码中用 $n+1 \sim n+k$ 表示）